Posts

Neural Networks and Machine Learning - IPS Cloud

Artificial Neural Networks and Machine Learning

Seen from the outside, an artificial neural network is a program run by a computer. Its peculiarity compared to other programs is the ability to learn the relationships between the input data and the output data (the results), this is obtained through a basic logical structure that does not change as the data and relationships vary, but it adapts to them.

The name neural network comes from the comparison with that of our brain. Its structure provides a series of points, called nodes, connected to each other, which receive a numerical value from other nodes, increase or decrease it and return the result to new nodes. Similarly, neurons in our brain receive an electrical impulse from a series of neurons and can retransmit or not this electrical impulse to other neurons. After this explanation, a neuron doesn’t seem like a very intelligent object. It gets small shocks and all it does is relay them or not to other neurons. How can all this current spinning in our head turn into such complex actions we can perform? The secret lies in the quantity. For example, if we had 100 neurons, not only we would not be very intelligent, but, considering that we are made, they would not even be enough to keep us alive (however there are animals that do not have any neurons, such as sponges). What if we have 1000? It wouldn’t make much difference, just think that a jellyfish has about 6000 and belongs to the category of fauna with the smallest brain capacity. A mouse already has around 70 million and we humans reach 86 billion. But how does quantity transform such a basic and banal process into the amazing abilities we possess? To get to the answer, let’s analyze an artificial network.

The artificial neural network

Diagram of a simplified artificial neural network

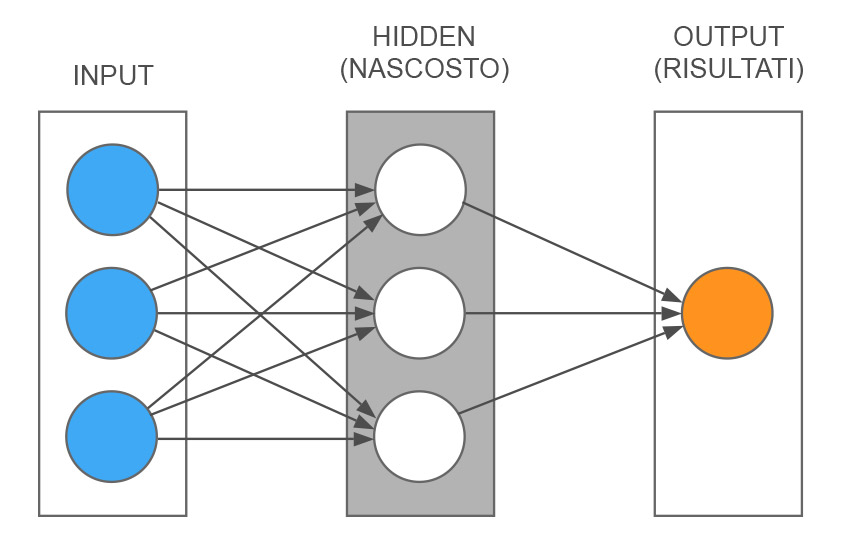
Diagram of a simplified artificial neural network

Let’s start by schematizing an example of a very simple neural network to understand its mechanism in detail. As you can see in the figure, we have three levels. One of the inputs, where, in this case, there are three nodes (blue circles), these three nodes represent three input information. A central level, called hidden because it does not communicate directly with the outside (white circles). And a layer on the right that represents the results, in this case, made by a single node (orange circle). The gray lines show the connections between the various nodes. The simplest way to explain how it works is with an example.

An example of a weather forecast

We use an extremely simplified weather forecast model. Suppose we want to forecast if it will rain or not an hour from now, based on three simple factors: 1) The number of clouds in the sky, 2) The wind speed, 3) The possible amount of rain at this moment. Our three inputs will be decimal numbers that can go from 0 to 1. For example, for the first factor, the number of clouds, we will have a 0 if there is no cloud in the sky, a 0.5 if the clouded areas and the clear ones are equivalent, up to 1 in the case in which the whole sky is covered with clouds. So we can see our cloud value as the percentage of the sky covered by clouds. We will do the same for the other two factors, i.e. the wind factor, which will be 0 in case of total absence up to 1 in case of maximum speed (the maximum speed will be defined a priori depending on the geographical area where we are making the forecast). Finally, we assign the value of the amount of rain, 0 in case of total absence up to 1 for the maximum intensity. To keep the example as simple as possible we have only one result and we call it raining.

The hidden level

Now that we have decided which are the inputs and outputs of our neural network, we can proceed to explain what this elusive intermediate level does. As you can see from the figure, each of the white dots (that represent neurons) receives all three inputs. So each of these nodes receives three numbers between 0 and 1. The first thing it does is assign a “weight” to each of these three values. This means that it defines a percentage for each of the inputs. Then it calculates these percentages and adds them. Let’s see an example.

Let’s take these three inputs: Clouds = 0.8; Wind = 0.1; Rain = 0.3. We are in a very cloudy sky, with very little wind and a little rain. The first node decides to give the cloudiness a weight of 35%, the wind a weight of 52% and the rain a weight of 2%. So the input values of this node will become 0.8 x 0.35 = 0.28; 0.1 x 0.52 = 0.052; 0.3 x 0.02 = 0.006. After doing these calculations, the node adds up the three results: 0.28 + 0.052 + 0.006 = 0.338. I guess you are asking yourself two questions, where did it take those percentages to calculate the weight of each input? Why does it do this? We begin to answer the first, for the second the answer will come later. These percentages are random. Well, you will say, everything already seemed not intelligent before, now that it makes up numbers it just seems pointless. In reality, we can say that at this point in the process, our system is ignorant, because it has not yet used intelligence to learn, but it will.

The next step is to define a threshold, that is a minimum value beyond which this information will go forward or not. In this case, for example, we can define that if the result of the calculation of a node exceeds 1.5 then the signal is transmitted over, otherwise it stops there. Also for this value, we don’t know a priori which is the correct one for each node, so we could set any number. However, in this case, I introduced the result of my reasoning into the neural network, choosing the average of the sum of the inputs. In our example, the sum of the three inputs can range from 0 (when they are all zero) to 3 (when they are all one). I did this to show how it is possible to start a neural network with parameters that already make sense, therefore knowledge and reasoning come from outside the neural network. The advantage of doing this is simply decreasing the time the network will take to get to the results, but it is not at all a necessary thing. To mathematically obtain the continuation or not of the information, we introduce a function that generates the value 0 if the result of the previous calculation is less than 1.5 or generates a 1 if the result is greater than this threshold. Then a 0 or a 1 will exit the node.

The results of artificial thinking

Now we are at the last level, that of the result. Each central node is connected to the result node, which we called raining. This node receives a 0 or a 1 from all the central nodes, exactly as before, it applies a weight to each incoming value and has a threshold value, under which the same mathematical function will generate a 0, and above it will generate a 1. So nothing different than the previous level. We were at the point when the first node of the central level calculated the value 0.338, which is less than 1.5, so it sent a 0 to the result node. Therefore the result node received a 0 from the first central node. Let’s say it applies to it a weight of 71%, so it gets 0 x 0.71 = 0. Similarly, it received the values from the other two central nodes, so we assume the other values with their weight and do the same sum we did for the central nodes: 0 x 0.71 + 1 x 0.27 + 1 x 0.95 = 1.22. In this case, without doing any reasoning, we decide that the threshold of this node is 2, therefore being 1.22 less than 2 our mathematical function will generate a 0. What does it mean that the node of the result raining is equal to zero? We decide what it means, and we say that if the value is 0 then it will not rain in an hour, whereas, if it is 1 it means that it will rain in an hour. In this example, our neural network told us that it will not rain. If the process ended here it would have the same value as tossing a coin and deciding that heads mean it will rain and tails no, so now we need to make our neural network capable of learning.

Machine learning

To allow the neural network to learn what relationships there are between the input information and the results, we need real data. In our example we have to collect data on cloud coverage, wind speed and rain intensity for a certain period of time. With this information, we have both the inputs and the results, because, if we collect the data every hour, we know that the intensity of rain at a certain time is what I should have predicted an hour earlier, so I am going to correlate it to the three parameters of the previous hour. In our very simple case, the result is not even intensity, but simply the presence or absence of rain. Once I have a good amount of data (obviously the larger it is, the more reliable the predictions will be), I apply what is called the error back-propagation to the neural network.

In other words, it is nothing more than a kind of trial-and-error learning. When the network works on the historical data series, it can make a comparison between the results obtained and the real data. In general, there will be a difference between the two values, therefore an error. The purpose of learning is the same as for a human being, to stop making mistakes, or better, to reduce them as much as possible. In our very simplified example, the neural network could calculate a 0 when the correct result had to be a 1, so no rain when it actually rained (and vice versa). Let’s assume that out of 100 real measurements, in 30 cases the result is correct, while in the remaining 70 it is wrong. To reduce the percentage of errors, the neural network can modify the parameters we saw earlier: the weight of the inputs and the threshold that determines whether the output of the node is 0 or 1.

How to optimise the parameters
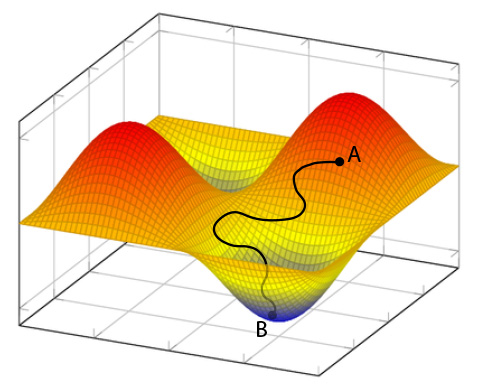
Example of a function that represents the error of the result in relation to weights and thresholds, that is, the parameters that the neural network can vary.

Example of a function that represents the error of the result in relation to weights and thresholds, that is, the parameters that the neural network can vary.

A first hypothesis is to continue modifying randomly these values for each node until the error drops below a certain level that we consider acceptable. By doing so we would have a neural network that has learned the correlations between inputs and results. This system could perhaps work for our example composed of a handful of neurons, but think of a network made up of hundreds of thousands of nodes, surely a lifetime would not be enough to see the result, most probably it would go beyond the duration of the universe from its birth to now. Then we have to think about smarter ways to find the correct parameters. We can use a mathematical function that contains our parameters and represents our error, and what we have to do is find where it is minimum (and therefore where the error is minimum). In the image we see an example of an error function in two variables: a curved surface with maxima and minima (peaks and troughs). What we need to do is change our parameters to get to the bottom of the lowest trough. In this case, we assume that with the initial parameters, which cause an error of 70%, we are in point A. We must find a way that, in the shortest possible time, takes us to point B, where we find the parameters that give the minimum error and make our network capable of making this weather forecast. To obtain this, there are very effective mathematical methods, such as stochastic gradient descent. Understanding these methods implies a substantial mathematical study and the purpose of this post is to explain the general concept. I have put the Wikipedia link for the more curious and stubborn readers who wish to delve into the subject.

More complex networks
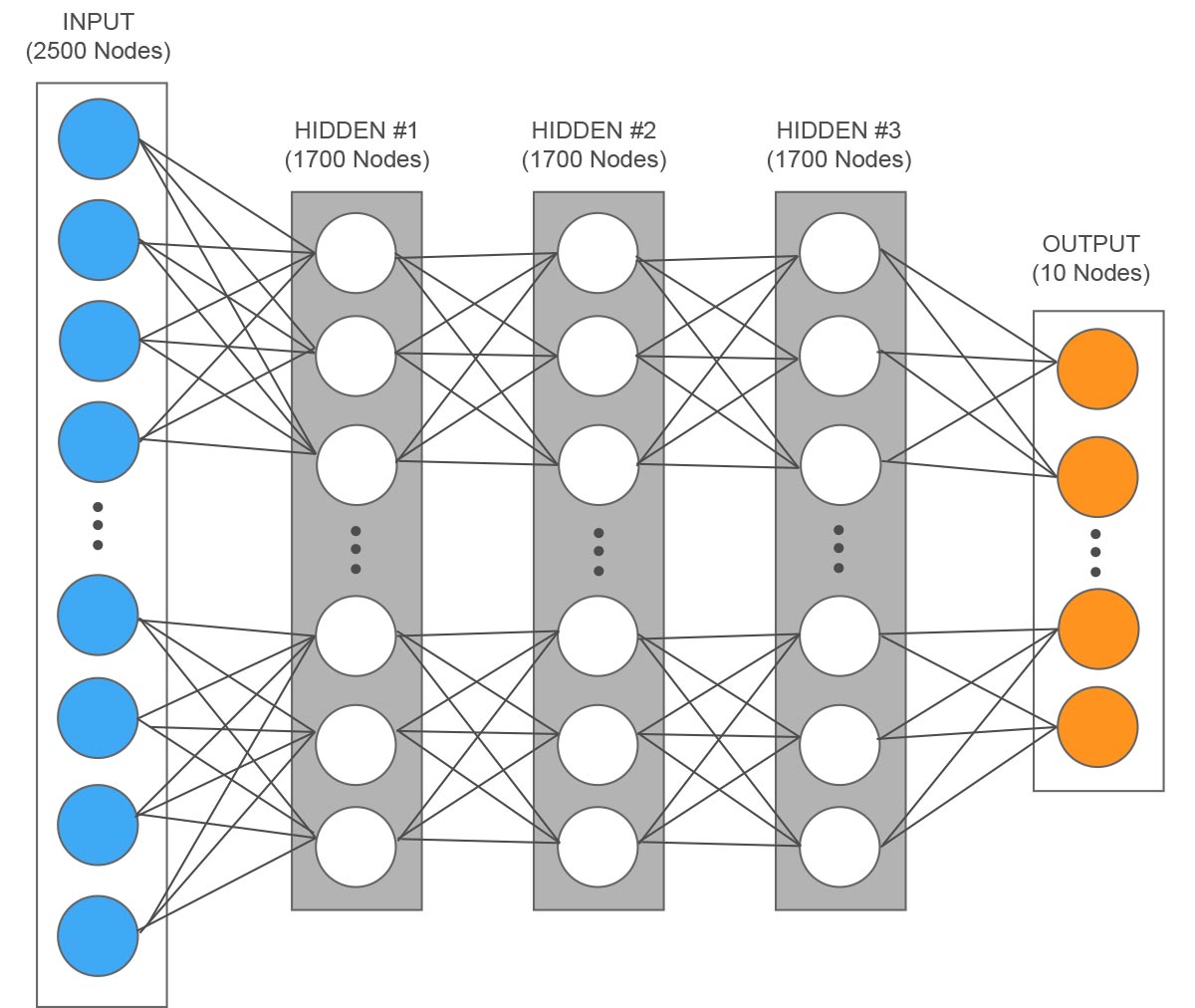
Example of a network for the recognition of handwritten digits with a resolution of 50x50 pixels

Example of a network for the recognition of handwritten digits with a resolution of 50×50 pixels, each input represents a pixel.

Now our network has the correct parameters, so it has learned what the relationships between inputs and results are and is able to predict if it will rain in an hour with a contained error. This example is extremely simplified, in reality neural networks can handle a much higher number of inputs and the results can also consist of multiple neurons. The intermediate level can be composed of several levels, where each one does a part of the work and passes the partial result to the next level. Let’s take the example of a network that recognises handwritten numbers, where a single digit is an image consisting of 50 x 50 pixels, so it would have 50 x 50 = 2500 input values. Let’s assume three intermediate levels, each composed of 1700 neurons and 10 for the results (the ten possible digits from 0 to 9), would be 5110 neurons in total. Now we can calculate how many parameters there would be to be optimised with each neuron of a level connected to all neurons of the previous level: 1700 x 2500 (weights) + 1700 (thresholds) + 1700 x 1700 (weights) + 1700 (thresholds) + 1700 x 1700 (weights) + 1700 (thresholds) + 10 x 1700 (weights) + 10 (thresholds) = approximately 10 million parameters. A final point to note is that in addition to the increase of neurons and connections, artificial neural networks can work together with other algorithms, creating a more efficient hybrid system.

Why the size makes the difference

Let’s go back to the question we asked ourselves at the beginning. Now that we have an idea of the operating principle of a neural network, we can also understand why a greater number of neurons implies greater skills. Actually, we should also talk about the number of connections. Thanks to them it is possible to have very complex mixes of inputs and therefore the possibility of manipulating in a more refined way what enters a neuron. We must think that a neuron does an extremely simple operation, so if we want to obtain a complex capacity, we must divide it into a certain number of elementary operations, which, combined together, will be able to give the result. If I have many input values, as in the example of the image of the handwritten number, in order to manage them all and not lose information, the number of neurons must be high. Let’s try to exaggerate and put only one neuron in the intermediate level, it will receive altogether the information of the 2500 pixels. It will only be able to vary their weights before adding them all, in this way, however, it will only have a value that will be an average of all the individual values, which says absolutely nothing about the image. If, on the other hand, we have more neurons, the first will only be able to give more weight to certain pixels and send that information forward, the second to others, and so on. In this way, the information is not lost and is processed more and more at each step up to the last level, that of results, where the neuron corresponding to the recognized figure will release the value 1. This division of tasks between neurons is obtained with the learning phase and the relative optimisation of the parameters as we have seen in the previous paragraph.

Lack of intelligence or learning?

Let’s give an example of the human brain. You went abroad, to a country whose language you absolutely do not know. A person approaches you and speaks to you in this language, your brain processes all the sound information received from the ears, each neuron is activated or not by the set of electrical impulses and, depending on the threshold, sends information or not to the following neurons. and so on until the results. But the results won’t make sense, they’ll just be a jumble of unknown sounds, even though your brain has done the same job it always does. The difference compared to when we listen to a dialogue in a known language is that in this case the learning part is missing, where all the parameters are set to process the inputs and give a useful result. Also in this case all the information coming from the person who spoke to you was lost, but unlike the example of the single neuron, that could not process the information of 2500 pixels by itself (lack of intelligence), in this situation, the number of neurons would have been enough, but the previous learning phase was missing.

 

In the next post, we will talk about what concrete results can be obtained with an artificial neural network and its main practical applications with the enormous benefits it brings.

The evolution of artificial intelligence - IPS Cloud

The evolution of artificial intelligence

Many people think that computers were invented after the discovery of electricity. In reality, the firsts were mechanical and dated back to the second half of the 1600s and were already able to carry out operations of addition, subtraction, and multiplication. But it was in the thirties of the last century that the foundations for computers and information technology were laid as we know them today. Claude Shannon, from Yale University, showed the potential of using the binary system in telecommunications and started what we now call the digital age, made of ones and zeros. In the same period, Alan Turing (famous for having deciphered the codes created by the German Enigma machine during World War II) published an article about the Turing Machine, a theoretical machine capable of executing algorithms (a procedure of logical instructions) and managing data. What Turing defined in this paper is still the basis of our computers today.

The machine that imitates man

Already during the forties of the last century, people talked about artificial intelligence (even if the name was born during the fifties). Artificial neural networks were born, at least on paper. It had been demonstrated that any computable problem, that is solvable by an algorithm, was solvable with a network of neurons. This network was made up of elements that could be “off” or “on”, and the state of each element was determined by the set of stimuli from the surrounding neurons (we will talk more about neural networks in the next post). In 1950, two Harvard students, based on the discoveries made in the previous decade, created the first rudimentary artificial neural network which they called SNARC (Stochastic neural analog reinforcement calculator). In the following years, a group of ten researchers led by John McCarthy took up the challenge to build a machine that would imitate the learning and intelligence of the human mind in all respects, and all to be completed in two months. Surely you are thinking that their ambition went a little beyond reality and I don’t think I need to tell you how it ended. Unlike them, Allen Newell and Herbert Simon, thanks to a more realistic but still surprising goal for the time, had already managed to build a machine that was able to prove mathematical theorems. In addition to having made various contributions to this subject, McCarthy is the author of the term artificial intelligence, which, from its first use in 1956, officially gave birth to the discipline of the same name.

Ambitions and difficulties

Imagine the enthusiasm that this newborn discipline created. The ability to realise machines able to reason seemed to have catapulted science fiction into reality. The first attempts were very promising. It was possible to prove even very complex geometry theorems and in 1966 James Slagle of MIT (Boston) succeeded in creating a program that solved integrals. This is not an easy operation and I think we can all confirm it by thinking of when we were in high school or university and we faced examples that we just hadn’t got a clue about how to solve. Unfortunately, all this euphoria died down soon. The researchers realised that in reality it was enough to increase the complexity of the system, even slightly, and the computational time became unsustainable. For example, if we apply a resolution system (which can be neural networks or another type of algorithm) to find the value of a variable and we say that in a few hours of computation we arrive at the result, by increasing the number of variables, this time can become longer than the age of the universe. This can depend on both the type of algorithm or system that is used to find the solution, and the computing power of the machine used. Sometimes it is even enough to increase the number of variables from one to two to make the system unsolvable in a reasonable time. For this reason, during the sixties, the interest in artificial intelligence faded and the funds were progressively cut.

From the 80s to now

In the 80s there was a rekindling of this discipline, the spark was fired thanks to the transition from the academic to the industrial world. In 1982, the first commercial intelligent software was used. It was a system to manage the sales of computers, able to recognize if there were missing components in an order. To do this, it had to understand and analyze the relationships that existed between the various components and manage any errors or deficiencies. This “toy” saved the company 40 million dollars a year. It didn’t take long before most of the big companies introduced intelligent systems to manage many different processes.

From 1986 there was also a return of neural networks, which remained somewhat on the sidelines after the limitations encountered during the sixties. New approaches were applied which led to promising results. Furthermore, in 1996 there was the famous chess victory of the computer Deep Blue (built by IBM) against the world champion Kasparov. Although this machine did not use neural networks, it was anyway huge publicity for the machine that imitates and surpasses man. A year later the intelligent systems landed at NASA, which used them to manage various aspects of space missions.

Today, intelligent software is making its way into all sectors. Think self-driving cars or sales forecasting systems. From weather forecasts to failure predictions in industry, passing through finance. Everything is transforming and becoming smart. The loT (internet of things) is leading to the connection of more and more objects to the network, therefore more and more data to be interpreted and exploited to improve efficiency, as well as the ability to remotely control everything. Intelligent systems lead to a breakthrough in the management of what is called Big Data and allow us to partially replace humans in making predictions, as well as optimizing complex systems.

Where will the future lead?

Today, artificial intelligence is able, for example, to recognize a person’s face or spoken language, but it is still far from many other characteristics of the human mind. This doesn’t make its possibilities less surprising or less effective, as we’ll see more in future posts, but if the question is how close it is to a human’s mind, the answer is not much. Many have speculated on where research in this field will arrive and when, but obviously, there is no certainty. Looking at the technological evolution over the centuries, we see an exponential trend. Homo sapiens took 150,000 years to arrive at agriculture with permanent settlements, only 7,000 to build the first empires, and science as we know it today was born just 500 years ago. As we saw at the beginning of the post, the IT era is about a hundred years old and only in the last 40 it has had a dizzying evolution. Looking at this trend, one would think that if it will continue in this way it would not be so strange in a hundred years to witness (for our posterity) machines capable of replicating all or almost all the skills of the human mind. And if we got to that point, maybe we could go even further, with machines that are much more intelligent than humans. On one hand, this fascinates, but frightens on the other. With such a scenario, would human beings still be at the top of the pyramid on our planet? We leave science fiction to answer this question, which has already given vent to many fantasies with the most disparate scenarios.

What is artificial intelligence? - IPS Cloud

What is artificial intelligence?

We often hear about artificial intelligence, but what it is and what its real potential is, is not always clear. The purpose of this and the following articles is to try to clarify and define its boundaries, up to its practical applications and advantages.

Let’s start with intelligence

First, we should try to define what we mean by intelligence, and this is far from being a simple task. Let’s start with the etymology of the word: intelligence comes from the Latin intelligere, which means to understand, to comprehend. We can see it as the process of passing from not knowing how something works to its understanding. I don’t think anyone could object that Newton used intelligence to understand what lies behind an apple falling to the ground, and he used intelligence to understand that its dynamic is the same as the dynamic of the moon rotating around the earth or the latter around the sun. But if I asked you if a newborn needs intelligence to learn how to walk, what would you answer? Or if our dog approaches and licks us because he understands that we are sad or suffering, is that intelligence? I am sure that for these last two questions, I would not have the same answer from everyone. This makes us understand how intelligence is a concept that can be interpreted in different ways and different people can decide to define more or less wide boundaries

We could go even further and ask ourselves if the living beings, who made an effort to move out of the water and “learn” to breathe the air, did so thanks to intelligence. In this case, I believe that almost everybody would say no. Because it is an evolutionary process, dictated by mutations and random facts, which brought aquatic beings out of the oceans after many generations. But even primitive man has learned to cook food thanks to random events, as scientists today can discover and learn something thanks to chance or more or less fortuitous attempts. Therefore, could we see the whole evolving living beings as a kind of global intelligence? I don’t want to try to answer this question, but I wanted to go up to this extreme to try to get rid of the prejudices we could have about the meaning of a term and be able to grasp many more facets.

Man-machine comparison

One feature that still surely distinguishes us from machines is the awareness of what we know and what we do. This does not mean that we are aware of everything we do (especially someone, you’d say…). Think of actions such as walking, taking an object with your hand, and so on. These are actions behind which there is no logical reasoning, that would give us a method to elaborate the way to coordinate thousands of muscles and carry out such a complex act. In fact, it seems very simple, we don’t even have to think about it. How many of you happened to be driving your car on your way to work and at some point wondering how you got there? As if your mind had done everything except thinking about driving and where you were going. We can say that we worked on autopilot. But it certainly wasn’t like that the first time you got behind the wheel, the process was much heavier, you had to understand, think, and learn. This denotes how many skills, that do not require reasoning, have become so after a learning process. Therefore, we could say that driving a car requires intelligence. In the first phase, to create the procedure in our memory and then to be able to use it, allowing us to manage all the sensory inputs involved and obtain the result of getting to work safe and sound.

We can summarize that in living beings there are innate abilities (developed through evolution), others that can be learned and transformed into automatic behaviours, and qualities that require the ability to find logical connections between things that apparently seem disconnected (they are those that allow us to discover new things). The time has come to ask ourselves which of these characteristics are typical of machines as well. The answer is all of them. This does not mean that machines can equal human beings in all their intellectual abilities, we are still extremely far from this goal, but it means that they are able to imitate the human mind in some of its capabilities.

Innate abilities and learning

We can look at a machine running an algorithm (a procedure of logical instructions) as an innate ability. Meaning that the computer, as a whole of hardware and software, was built and programmed to perform a certain task. Unlike human beings, it did not autonomously evolve to become what it is today, but it is the product of the cultural and technological evolution of humans. This feature has great potential if we think that it allows machines to obtain results that human beings cannot achieve. This is so thanks to their great speed, to the fact they can have powerful sensors and operate without resting. Let’s think of the security systems that read your retina and compare it to samples in fractions of a second; or to navigation systems that calculate the fastest route for distances of thousands of kilometers in few seconds. These are things that humans are not able to do or even learn, because our characteristics do not allow it. Maybe it would be a bit of a stretch to call this intelligence, but we could see it as a transfer of the human intellect into the capabilities of the machines. Again, I want to dare and try to define the human-machine sum as an entity a little more intelligent than the human alone.

What is really interesting is that a machine is also capable of learning and can do it in a similar way as the human brain. One of these systems is called artificial neural network. In the next posts we will briefly retrace the evolution that in the last century has led us to this point. We will then go into a little more detail, explaining the functioning of these neural networks and how far they have approached the brain’s capabilities, to conclude with the practical advantages they bring to the industrial world.